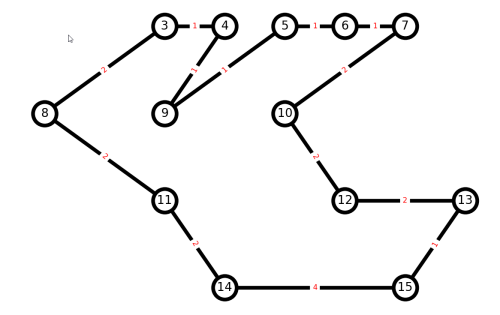
Let us create a small imaginary trail graph in Python with NetworkX, and play around with plotting and paths. Suppose we have a graph with nodes from 0 to 15:
import networkx as nx
import matplotlib.pyplot as plt
G=nx.Graph()
edges=[(0,1,1),(1,2,1),(2,3,1),(3,4,1),(4,5,1),(5,6,1),(6,7,1),
(8,3,2),(9,4,1),(9,5,1),(10,7,2),
(8,9,2),(9,10,2),
(8,11,2),(12,10,2),
(11,12,2),(12,13,2),(13,7,2),
(11,14,2),(14,15,4),(15,13,1)]
G.add_weighted_edges_from(edges)
The tuple (8,11,2) means an edge goes from node 8 to node 11, with weight 2.
Now we specify where the nodes are located.
#pos=nx.spring_layout(G) does not give satisfactory results.
# Draw node positions the hard way.
pos=[(0,4),(1,4),(2,4),(3,4),(4,4),(5,4),(6,4),(7,4),
(1,3),(3,3),(5,3),
(3,2),(6,2),(8,2),
(4,1),(7,1)]
We are almost ready to draw the network. Since we want to draw weights for the edges, we have an extra step.
options = {
"font_size": 16,
"node_size": 1000,
"node_color": "white",
"edgecolors": "black",
"linewidths": 5,
"width": 5,
}
nx.draw_networkx(G, pos,**options)
labels = {e: G.edges[e]['weight'] for e in G.edges}
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels, font_color="red")
plt.show()
And here is our result.
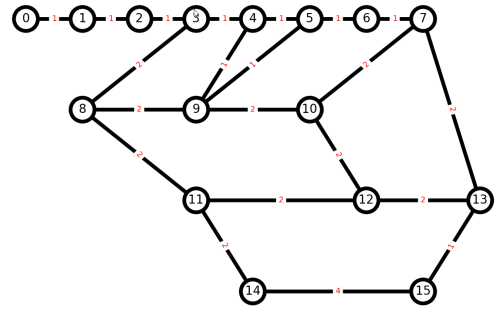
Think how we can convert this into a Euler graph, so all nodes have an even number of edges. We can try a Networkx library function, but should not expect it will do what we want, because it will create a multigraph, with more than one edge between nodes.
H = nx.eulerize(G)
Our command to plot the resulting graph has to be a bit more complicated, to allow for showing more than one edge between pairs of nodes. [hat-tip]
nx.draw_networkx_nodes(H, pos, node_color="white", node_size=1000)
ax = plt.gca()
for e in H.edges:
ax.annotate("",
xy=pos[e[0]], xycoords='data',
xytext=pos[e[1]], textcoords='data',
arrowprops=dict(arrowstyle="->",
color="0.5",
shrinkA=5, shrinkB=5,
patchA=None, patchB=None,
connectionstyle="arc3,
rad=rrr".
replace('rrr',str(0.3*e[2])
),
),
)
plt.axis('off')
plt.show()
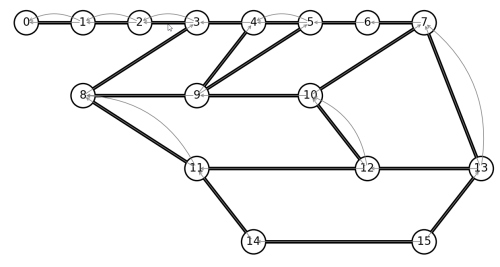
Well, we expected to eliminate nodes 0-2, as a dead-end on our Euler path. After that, there are 4 pairs of nodes with multiple edges. If we remove every double-edge, we hope to still have an Euler graph. Let’s write code to remove all double-edges. Python does not like when we modify a graph during a for-loop, so a better practice is to create a new graph, copying all edges that are not double-edges.
J = nx.Graph()
for node in H.nodes():
# We look for adjacent nodes
neighbors = H.neighbors(node) #Find all neighbors of node n
for adj_node in neighbors:
if len(H[node][adj_node]) == 1:
# get weight of the edge
w = H.edges[node,adj_node,0]['weight']
J.add_edge(node, adj_node, weight = w)
A subtlety here for newbie NetworkX users like myself is to use
>> H.edges[node,adj_node,0][‘weight’]
instead of
>> H.edges[node,adj_node][‘weight’]
because H is a multigraph, and could possibly have more than one edge between each pair of nodes. Since J is a simple graph, it should not matter if we add an edge twice, since the edge would just get overwritten. Plotting the result:
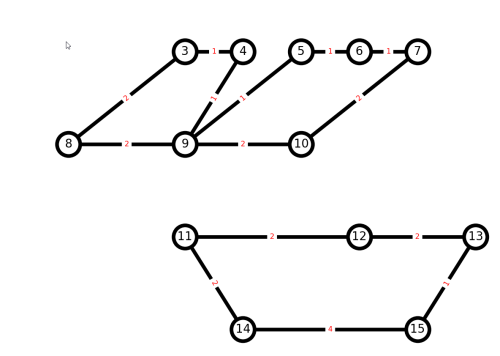
The output is not ideal, because our naive algorithm disconnected the graph.
Alternatively, manually choose better edges to delete , and defer the max-path algorithm to another post.
G.remove_edges_from([(0,1),(1,2),(2,3),(4,5),(8,9),(9,10),
(11,12),(7,13)])
G.remove_nodes_from([0,1,2])
print("Is G an Eulerian graph? : ",nx.is_eulerian(G))
print(list(nx.eulerian_path(G,source=3)))
Is G an Eulerian graph? : True
[(3, 4), (4, 9), (9, 5), (5, 6), (6, 7), (7, 10), (10, 12), (12, 13), (13, 15), (15, 14), (14, 11), (11, 8), (8, 3)]