Sagebrush personal hiking blog
Several NMVFO project leaders met at Sisters Cities Park in Albuquerque to train on GMRS radios for use on our projects.
Until we all have cell phones with free satellite texting, this should allow us to communicate better on trails.
I listen to audiobooks while hiking solo, and have been fortunate enough to do a long hike each year since 2012– that is a lot of audio. I record links to each completed audiobook in my online hiking journals, first as a note to myself, and second a recommendation to anyone reading or crawling this blog, a shout-out to the work of authors and readers that I have enjoyed.
My preference is to avoid audiobooks with DRM Digital Rights Management, and unfortunately a monopoly controlling contemporary audiobooks insists on DRM as a condition for authors to be published with them. Luckily for me, LibriVox was started in 2005, a group of volunteer readers who record and distribute audiobooks of public domain books. In my youth I tended to read mostly science fiction, and missed out on many classics of literature, and LibriVox has allowed me to remedy that situation in some small part.
(Please be aware that book copyright duration differs according to country, and USA rules are different from everyone else. Nowadays I look forward to seeing what new books slip out of copyright January 1 of each year, for possible use on my next hike.)
Below are all the audiobooks completed on my long hikes to date, sometimes with short notes. Perhaps this might help other travelers on their audiobook journey. More notes below the list…
(no audiobooks on this trip, just podcasts)
When hiking, I only listen to audiobooks in one ear, at moderate volume, and take care to be aware of sounds around me. If I am in serious bear country, audiobooks can wait.
For USA copyright rules, in 2025 works published in 1929 or before move into the public domain. Due to a quirk in copyright law, many early science fiction whose copyright was not renewed by the publisher became public domain early, so I have recently been enjoying Golden Age SF.
I make a note of particularly good readers, and often seek out other books they have read. Some of my favorite LibriVox readers: Kara Shallenberg, Karen Savage, and the prolific Phil Chenevert. For the Girl Genius Agatha H series, Angela Dawe is excellent. For Cory Doctorow books, Wil Wheaton is super, though the author is also quite good. I avoid AI readers, for now. No narrators with uptalk, please.
On early hikes I also listened to contemporary audiobooks by Podiobooks.com, a site for mostly free downloads by self-published authors. Sadly that site has been absorbed by another website with a different business model, and links may not work.
During the lonely months between long hikes I keep up morale by searching for more audiobooks on LibriVox and elsewhere, and currently have more than 100 books downloaded for future hikes.
Ground Truth: Information known to be true by direct observation, rather than by inference. In GIS (Geographical Information Systems), ground truth refers to verifying or correcting data on a map database by going out and measuring.
Truthiness: Assertion that a statement is true based on opinion, without regard to evidence. (Coined by Stephen Colbert on the Colbert Report)
The 1.0 version of the Gila X Loop is not workable, and no one should attempt to hike this route in its present form. One key connector trail between Glenwood and Gila Hot Springs, Holt Apache Trail #181, is in questionable condition after a fire, likely very brushy with thorny locust. On my route #181 connects to Turkeyfeather Mountain Trail #102, which is completely removed from the USFS Gila Interactive Map, although it still appears on plenty of printed maps, CalTopo, GaiaGPS, and OpenStreetMap. Likely there are other trails on my route that are actually non-trails, permanently abandoned by the USFS due to serious damage after fire and subsequent erosion.
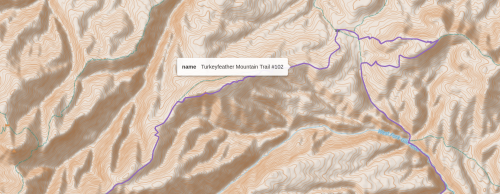
I will need to re-run my algorithm, after removing trails that are not on the Gila Interactive Map and no longer recognized by the USFS. Look for v2.0 of the Gila X Loop sometime in 2025-2026, along with an attempted thru-hike for even more Ground Truth.
On another matter, I encountered difficulty hiking on the Deloche/Winn Canyon Trail #179. My algorithm attempted to exclude “deloche and winn canyon” (case insensitive), but openstreetmap.org and most sources used the name “deloche/wynn canyon”. Computer programs typically look for an exact match when comparing strings. Oops.
Lessons Learned: