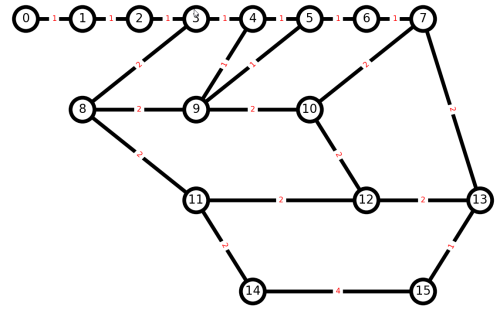
First off, I am no expert in Graph Theory, or of mathematics, or even computer science, so what follows may be completely and totally wrong, the Dunning-Kruger effect writ large. This is just me trying to get a reasonable approximation to the question posed in the first post in this series:
What is the longest continuous route on existing trails in the Gila National Forest, that does not repeat any segment (but intersections are OK)?
And what is the longest continuous loop?
The longest path problem is known to be computationally hard, and even getting a reasonable upper bound of compute time for unweighted cyclic undirected graphs is difficult. The computation time is likely to be excessive for an exact solution for our size graph, so let us settle for approximations. After all, as long as a long distance hiker has at least a 600 mile trip, that is long enough for a reasonable adventure, and if the journey could have been 20% longer with a faster computer, we beg the hiker to forgive us.
Start by considering the Chinese Postman Problem: A postman needs to visit every street (edge) in a town (graph) at least once to deliver mail. What is the minimum distance to be traveled in a circuit, allowing some streets to be walked more than once?
Find the shorted closed loop on an undirected weighted graph that visits every edge at least once.
Let us call a node with an odd number of edges an odd node. If we pair up each odd node with another odd node, and then duplicate the edges between those pairs of nodes, then all nodes have an even number of edges, and we get a Euler graph, and an Euler circuit. Iterate over all those possible pairings to find the pairing (matching) with minimum total distance.
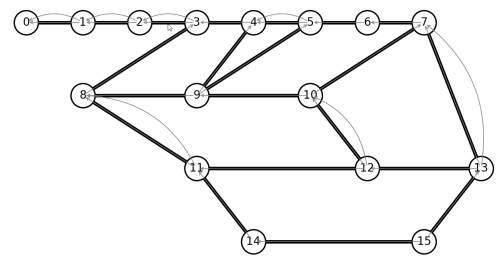
Now let us modify the Chinese Postman Problem to iterate over all pairings as before, but to look for a matching that results in a maximum distance. And because we do not want to repeat any trail segment, instead of duplicating edges between pairs of odd nodes, let us delete edges between odd nodes. (We may have more than one path between a pair of odd nodes, but perhaps we can choose the shortest path as a first-approximation). And another wrinkle, since we are deleting edges, we should be looking at edge connectivity as well as distance when deciding what edges to delete. Removing an edge might delete a large chunk of the graph.
Continue reading “Trails and Graph Theory 5: Algorithms”