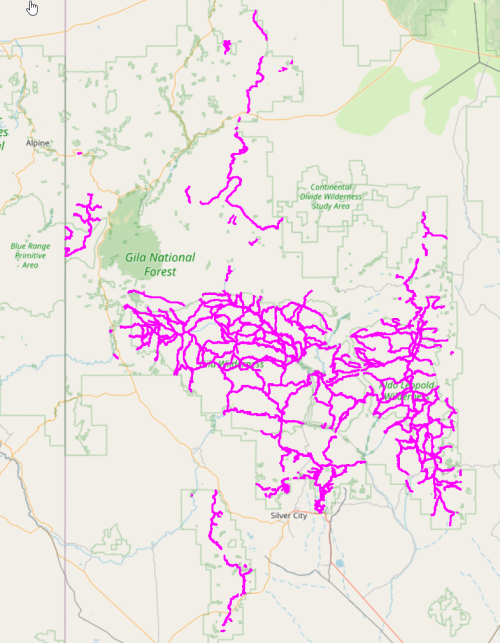
In our last post, we found a single Euler Graph that is a subset of the Gila National Forest trail system, but we were left with the question of how to find other, possibly better, solutions. We might try several alternatives, so the first thing is to save the input graph that we massaged by removing 1-nodes and collapsing 2-nodes from the full Gila trail graph, so we do not have to repeat that step each time we try something new. The Python library pickle is just what we need, as it will save any arbitrary Python object to disk so we only need to compute this initial graph once.
import pickle
pickle.dump(H,open('h_graph.pkl', 'wb'))
Recall that in a previous post we had found a function all_maximal_matchings(graph G) that should help us find candidates for longer Euler graphs than we found in our previous post. Unfortunately, for our size graph, the function is unbearably slow, so we have added a timing function to better gauge our progress.
import time, datetime
start_time = time.time()
def elapsed_time(start):
end_time = time.time()
duration = round(end_time - start)
timestamp = str(datetime.timedelta(seconds = duration))
print(timestamp)
We add an elapsed_time to each iteration in all_maximal_matchings(…) to see what is happening.
...
matching 805
not eulerian matching, length 60
1 day, 5:14:26
matching 806
not eulerian matching, length 60
1 day, 5:14:26
matching 807
not eulerian matching, length 60
1 day, 5:14:27
matching 808
not eulerian matching, length 60
1 day, 5:14:27
matching 809
not eulerian matching, length 60
1 day, 5:14:27
...Oof, over a day of computation, and no helpful results yet.
For n nodes, all_maximal_matchings() seems to be higher than order O(n³), too large for a graph with 128 odd nodes, and in practice the “worst” maximal matchings are discovered first. We need an alternative approach.
Recall that we used a library function networkx.algorithms.min_weight_matching() to find a single solution last time, and that function is rather fast, using the Blossom algorithm. As a first attempt, let us introduce some “noise”, or “fuzz “in the weights of the graph, and see if that results in alternate solutions that might be longer.
import random
def fuzz_min_weight_matching(Q):
T = nx.Graph()
for u, v, d in Q.edges(data=True):
len = d['length']
len = len * (1 + random.random())
T.add_edge(u,v,length=len)
return nx.min_weight_matching(T,weight='length')
We run this function many times, and see if we can find longer Euler loops. The results are displayed in an animated GIF file, using techniques adapted from the article Graph Optimization with NetworkX in Python. Each iteration we display a graph, and compare it to the current maximum length graph, using the function save_png(). Plotting onto map tiles is unnecessary, so let us simplify matters by drawing onto a white background.
def save_png(Q, max_Q=None, bounds=None, index = 0, iteration_label='', max_label='' ):
m = folium.Map()
QD = Q.to_directed()
QD.graph['crs'] = ox.settings.default_crs
nodes, edges = ox.graph_to_gdfs(QD)
ax = edges.plot(color='#ff00ff', label = iteration_label)
if max_Q != None:
QD = max_Q.to_directed()
QD.graph['crs'] = ox.settings.default_crs
nodes, edges = ox.graph_to_gdfs(QD)
edges.plot(ax=ax, color='y', linewidth=3, alpha=0.2 , label = max_label)
if bounds != None:
sw = bounds[0]
ne = bounds[1]
ax.set_xlim(sw[1], ne[1])
ax.set_ylim(sw[0], ne[0])
ax.legend(loc="upper left")
ax.plot()
plt.axis('off')
plt.savefig('fig/img{}.png'.format(index), dpi=120)
plt.close()
(The bounds code is necessary to ensure that each PNG file is the same size and displays exactly the same map coordinates, otherwise the graphs jump around in the movie.)
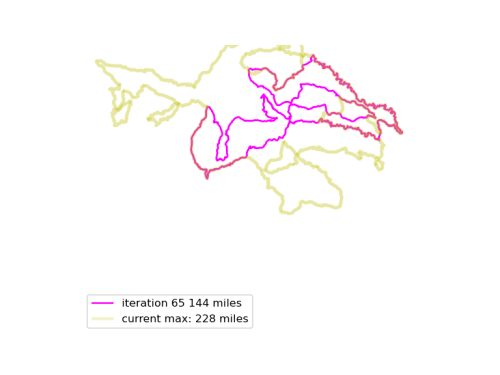
Now, combine all those .PNG files into an animated GIF.
import glob
import numpy as np
import imageio.v3 as iio
import os
def make_circuit_video(image_path, movie_filename, fps=5):
# sorting filenames in order
filenames = glob.glob(image_path + 'img*.png')
filenames_sort_indices = np.argsort([int(os.path.basename(filename).split('.')[0][3:]) for filename in filenames])
filenames = [filenames[i] for i in filenames_sort_indices]
# make movie
frames = []
for filename in filenames:
frames.append(iio.imread(filename))
iio.imwrite(movie_filename, frames, duration = 1000/fps, loop=1)
The resulting animated GIF is optimized and displayed below:
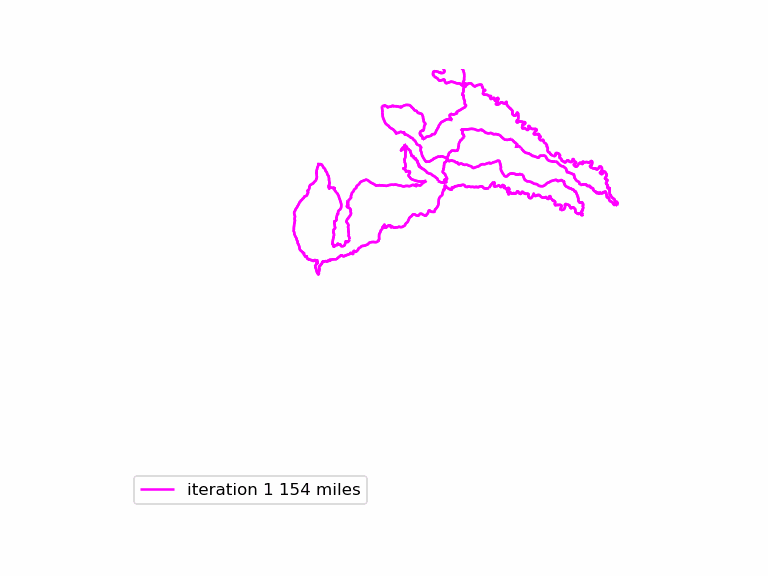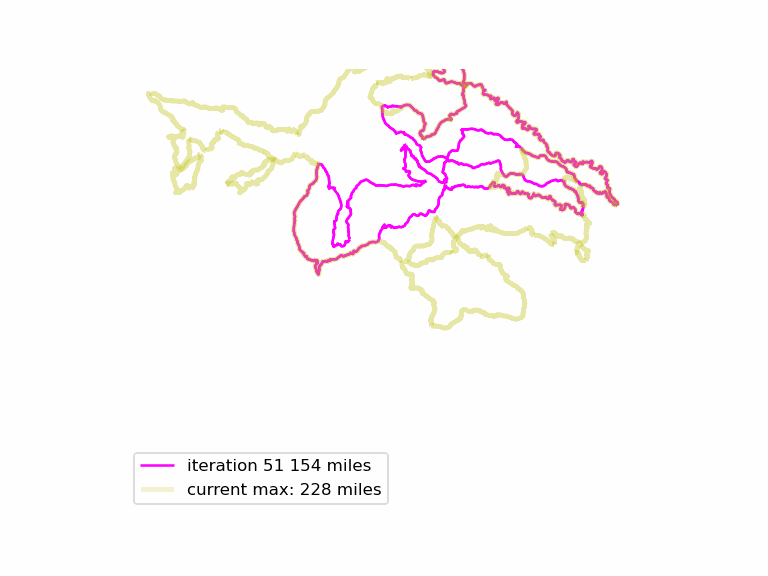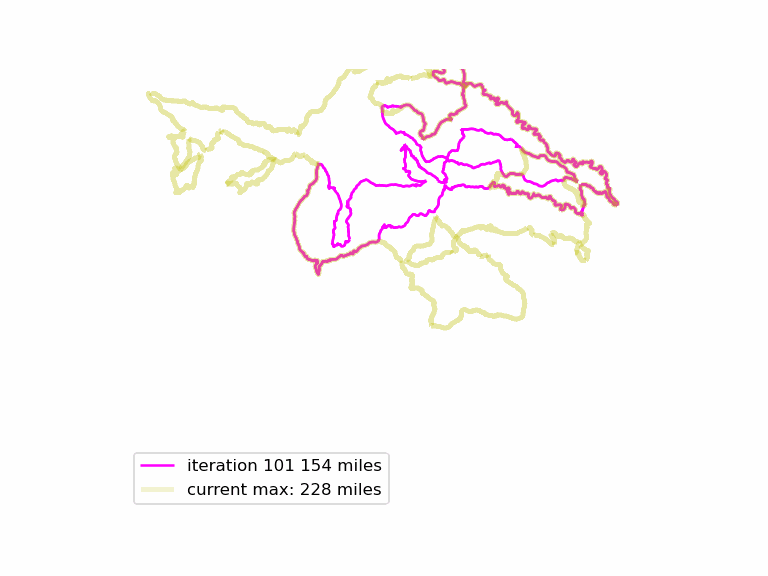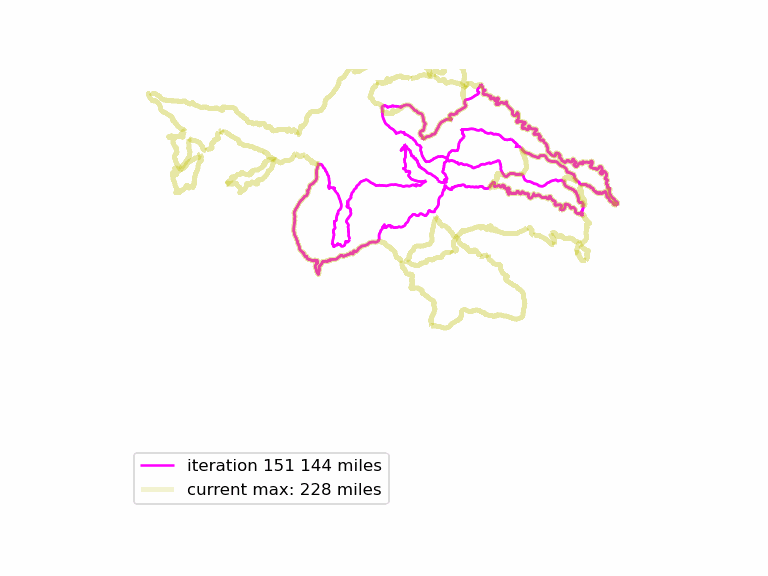
Download the complete source code for this article here.
What is next to try? Gradient fuzz? A genetic search? Fixing some fundamental error I missed? Stay tuned (subscribed) until next time…