A few utility functions were created to help solve our maximum-length trail problem. Since most of you may not be interested in the code, I will first describe what each function does, and then append the source at the end for you to skip over.
First is report(graph, description=”), which reports of the number of edges and nodes of a graph, and some basic statistics. We will use our first example graph as an example. We make a small change to start with a Multigraph instead of a Graph, and to use ‘length’ instead of ‘weight’, to be more compatible with OSMnx later.
report(G)
16 nodes
21 edges
total length 0.02 miles
number of odd intersections : 10
number of even intersections : 6
number of 2-way intersections : 5
number of trailhead/terminus : 1The function draw(graph, title=”) displays our simple graphs, and can handle Multigraphs.
draw(G)
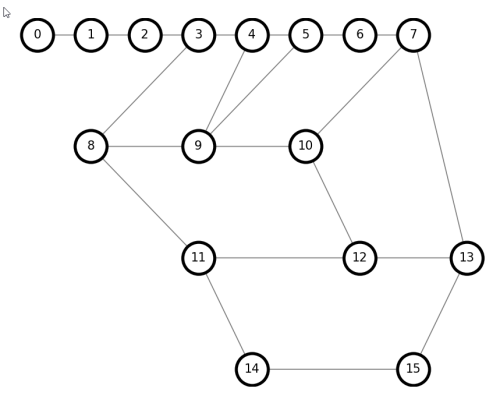
Trailhead/terminus points are dead-ends that cannot be included in a grand circuit, so it is computationally easier to eliminate them early, with delete_ends(graph).
delete_ends(G) report(G,'in undirected multigraph with ends removed')
13 nodes in undirected multigraph with ends removed
18 edges in undirected multigraph with ends removed
total length 0.02 miles in undirected multigraph with ends removed
number of odd intersections in undirected multigraph with ends removed : 8
number of even intersections in undirected multigraph with ends removed : 5
number of 2-way intersections in undirected multigraph with ends removed : 4
number of trailhead/terminus in undirected multigraph with ends removed : 0draw(G,'undirected multigraph with ends removed')
As expected, the number of trailheads/termini in the report is now 0.
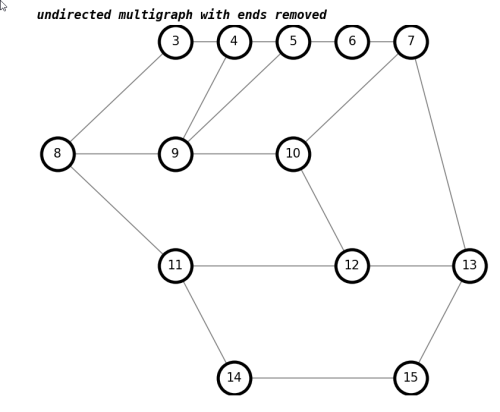
We will also merge nodes with only two edges, to make it clearer which three-way intersections are neighbors of each other, with contract_twos(graph).
contract_twos(G) report(G,'with two-nodes merged')
9 nodes with two-nodes merged
14 edges with two-nodes merged
total length 0.01 miles with two-nodes merged
number of odd intersections with two-nodes merged : 8
number of even intersections with two-nodes merged : 1
number of 2-way intersections with two-nodes merged : 0
number of trailhead/terminus with two-nodes merged : 0draw(G, 'two-nodes merged')
The number of 2-way intersections in the report is now zero, as we hoped.
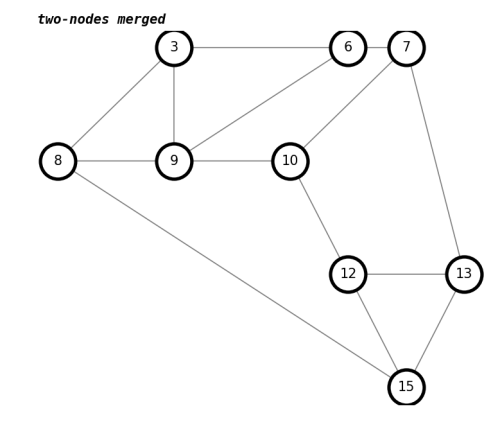
We will copy over all the 3-nodes to a new graph, so later we can match all odd nodes as pairs, with odd_nodes_graph(graph) .
K = odd_nodes_graph(G) >> report(K,'in odd-nodes graph')
8 nodes in odd-nodes graph
10 edges in odd-nodes graph
total length 0.01 miles in odd-nodes graph
number of odd intersections in odd-nodes graph : 4
number of even intersections in odd-nodes graph : 4
number of 2-way intersections in odd-nodes graph : 4
number of trailhead/terminus in odd-nodes graph : 0draw(K,'odd-nodes graph')
The report shows even nodes, because we have omitted some nodes, which reduces some edges. We will fix that later.
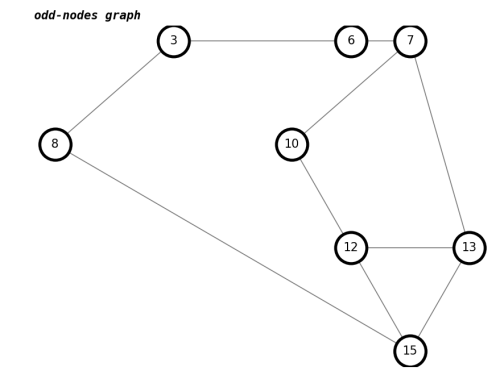
All the three-nodes that are connected to a 4-node are effectively neighbors of each other for our matching algorithm, so function complete_3node_graph( original_graph, three_node_graph ) adds in the extra edges.
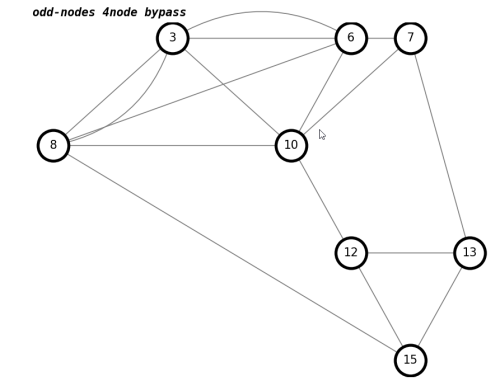
k_fix_4_list = complete_3node_graph(G,K) report(K,'in odd-nodes 4node bypass')
8 nodes in odd-nodes 4node bypass
16 edges in odd-nodes 4node bypass
total length 0.02 miles in odd-nodes 4node bypass
number of odd intersections in odd-nodes 4node bypass : 8
number of even intersections in odd-nodes 4node bypass : 0
number of 2-way intersections in odd-nodes 4node bypass : 0
number of trailhead/terminus in odd-nodes 4node bypass : 0draw(K,'odd-nodes 4node bypass')
Now we have a graph with only odd nodes, ready for matching.
We will use a built-in NetworkX function to suggest an optimal matching of odd-nodes.
odd_matches_set = nx.algorithms.min_weight_matching(nx.Graph(K),'length')
print('number of odd matches', len(odd_matches_set))
# delete matched edges
K.remove_edges_from(odd_matches_set)
report(K,'with odd-node matches removed')
number of odd matches 4
8 nodes with odd-node matches removed
12 edges with odd-node matches removed
total length 0.02 miles with odd-node matches removed
number of odd intersections with odd-node matches removed : 0
number of even intersections with odd-node matches removed : 8
number of 2-way intersections with odd-node matches removed : 4
number of trailhead/terminus with odd-node matches removed : 0draw(K,'odd-node matches removed')
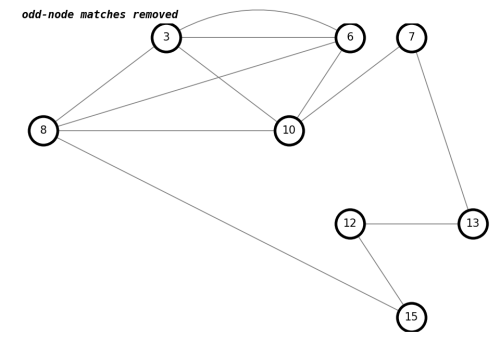
By deleting edges between matched odd nodes, we have a graph with only even nodes.
Later, we will add back in the 4-nodes with restore_4node_graph( graph, fix_4_list ).
restore_4node_graph(K,k_fix_4_list) report(K,'odd-matches deleted with 4nodes restored')
9 nodes odd-matches deleted with 4nodes restored
10 edges odd-matches deleted with 4nodes restored
total length 0.01 miles odd-matches deleted with 4nodes restored
number of odd intersections odd-matches deleted with 4nodes restored : 0
number of even intersections odd-matches deleted with 4nodes restored : 9
number of 2-way intersections odd-matches deleted with 4nodes restored : 8
number of trailhead/terminus odd-matches deleted with 4nodes restored : 0 draw(K,'odd-matches deleted with 4nodes restored')
We have added back in nodes with 4-way intersections, and still have a graph with only even nodes.
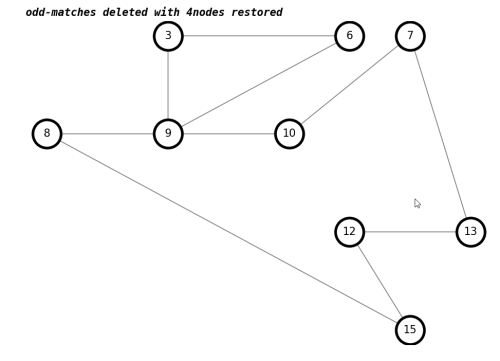
In this example, we see that the result is an eulerian graph, with no odd nodes. In the general case, we would expect the graph to splinter into subgraphs when we delete a bunch of edges, and we would look for the largest subgraph.
nodes = max(nx.connected_components(K)) L = nx.subgraph(K, nodes) report(L,'in largest subgraph with odd-node matches removed')
9 nodes in largest subgraph with odd-node matches removed
10 edges in largest subgraph with odd-node matches removed
total length 0.01 miles in largest subgraph with odd-node matches removed
number of odd intersections in largest subgraph with odd-node matches removed : 0
number of even intersections in largest subgraph with odd-node matches removed : 9
number of 2-way intersections in largest subgraph with odd-node matches removed : 8
number of trailhead/terminus in largest subgraph with odd-node matches removed : 0if nx.is_eulerian(L):
print('L is eulerian')
print('The node path is: ', [u for u,v in nx.eulerian_circuit(L)])
L is eulerian
The node path is: [3, 9, 10, 7, 13, 12, 15, 8, 9, 6]This solves the maximum path for our simple example graph! We came up with the same solution that we found manually back in Trails and Graph Theory 3: NetworkX (although we have merged some nodes to simplify computing).
If the canned library matching does not work, we can iterate through all the possible matchings (pairings) of 3-nodes and determine the optimum matching with find_best_matching( graph, filter ). I tried to write this function myself, without much success, but found a Stackoverflow post with just the code I needed, truly a thing of beauty, much more elegant and concise Python than I could manage. We may be using this code in the next post as we attempt to apply our functions to the Gila trail map.
The source code for these functions can be downloaded here, for the truly adventurous.