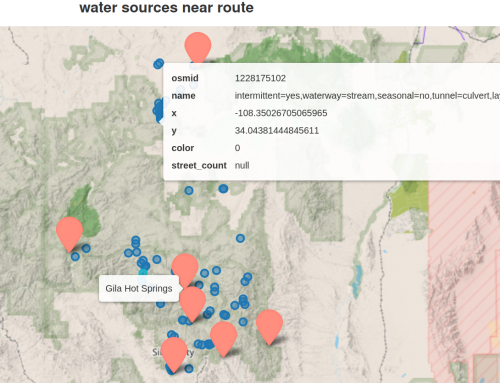
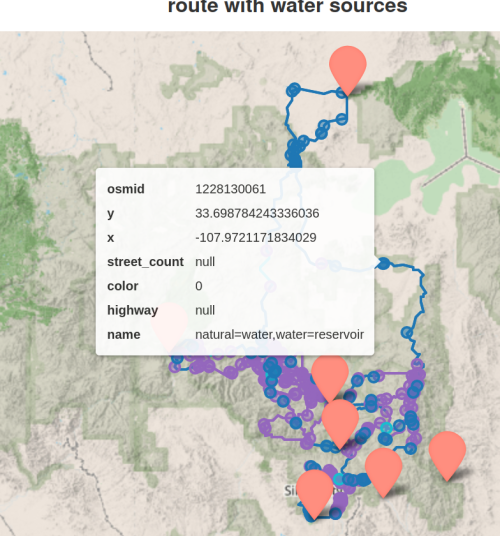
In a previous post we imported elevation information into our graph and databook, using a JSON query to an open data website.
#https://stackoverflow.com/questions/68534454/python-obtaining-elevation-from-latitude-and-longitude-values/68540685#68540685
def get_elevation(lat, long):
return 0
query = ('https://api.open-elevation.com/api/v1/lookup'
f'?locations={lat},{long}')
r = requests.get(query).json() # json object, various ways you can extract value
elevation = pd.json_normalize(r, 'results')['elevation'].values[0]
return elevation # returns in meters, not freedom units
Now, in preparation to revisiting our databook code, we will take advantage of the elevation module in OSMNX, reading in elevations for all nodes in the graph with one function call. (Even though the API call is add_node_elevations_google with ‘google‘ in the name, we are not required to use the Google service, for which I do not have a key).
ox.settings.elevation_url_template = 'https://api.open-elevation.com/api/v1/lookup?locations={locations}'
ox.elevation.add_node_elevations_google(J, api_key=None,
batch_size=350,
pause=1.0,
)
(If you use the service at open-elevation.com, please throw them a donation.)
We can colorize our nodes and edges by elevation, making the crude approximation that an edge elevation is the mean elevation of its two nodes.
def colorize_elevation(Q):
QR = Q.copy()
for node, dat in Q.nodes(data=True):
dat['color'] = dat['elevation']
QR.add_node(node,**dat) #replace node value
for u, v, k, dat in Q.edges(keys=True,data=True):
e1 = Q.nodes[u]['elevation']
e2 = Q.nodes[v]['elevation']
dat['color'] = (e1 + e2)/2.0
QR.add_edge(u,v,key=k,**dat)
QR.graph['color']=True
return QR
A small change to our draw() function uses magma as our pre-defined cmap.
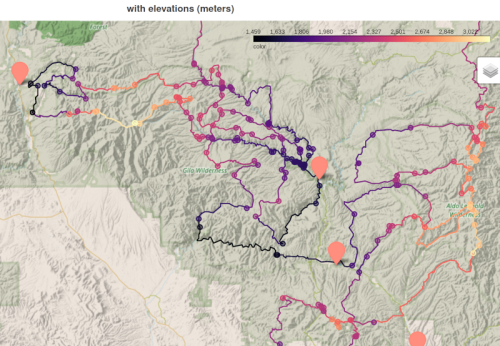
Because my graph is simplified, meaning many 2nodes are merged together, the elevation appears to have large steps. We will address this in the next post.
Download source code here.