It all started with a question:
What is the longest continuous route on existing trails in the Gila National Forest, that does not repeat any segment (but intersections are OK)?
And what is the longest continuous loop?
Can the result be mapped and documented as a Long Trail to share with hikers?
Sagebrush
The Gila has a few trails that dead-end, so those can be eliminated, and several trails are currently in poor condition due to fire or lack of maintenance, and not reasonable to hike. Furthermore, some trails are not where they are shown on published maps. Fortunately, I know an expert on the Gila, an individual with boundless energy who is dedicated to reopening and maintaining routes. And perhaps another published long trail could be used as a motivation to go out and work on particular segments.
Finding a longest route is an optimization problem, so mathematics might be able to help. A famous problem in math is the Traveling Salesman. One version:
A salesman needs to visit all lower-48 state capitals and return to the beginning. What is the route with minimum distance?
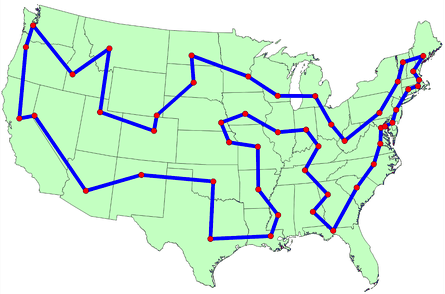
An obverse is the Longest Path Problem
What is the longest path in a given network?
Nano Intro to Graph Theory
Graph Theory is a branch of mathematics that can help us here. A graph has nodes (or points or vertices) that are connected by edges, and can be represented visually:
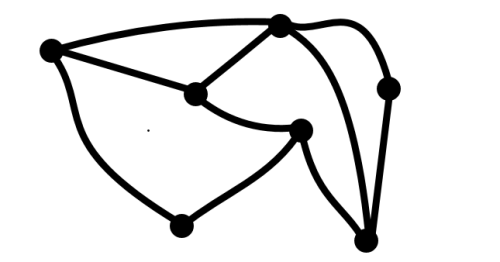
A graph can be a undirected graph, or directed. For trail systems, we will consider undirected.
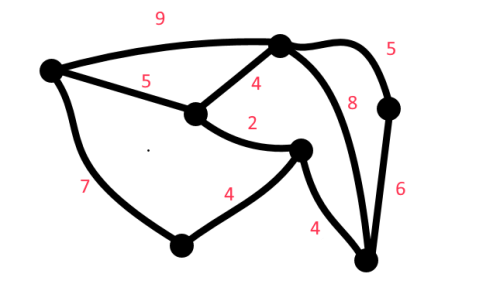
The edges of a graph can have weights, which could correspond with distances between intersections in a trail network.
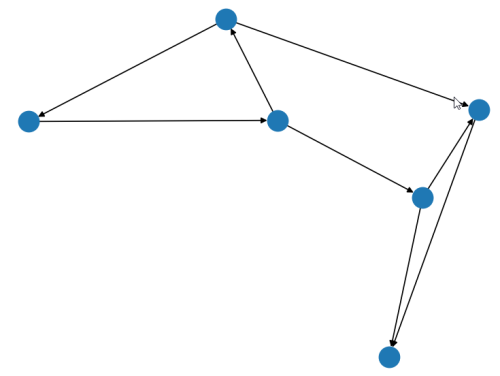
A path on a graph can be an ordered sequence of nodes and edges.
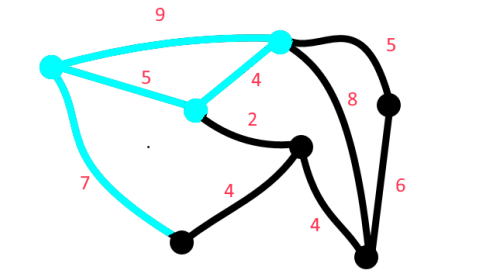
A path is defined as simple if it does not have any repeated nodes.
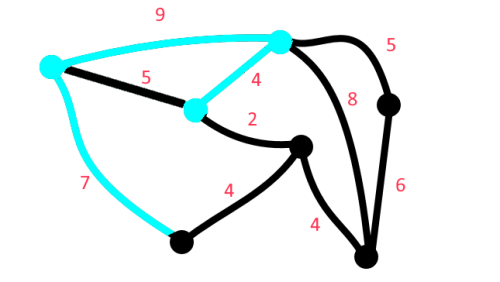
So for the Gila problem posed above, we consider a non-simple path on a weighted undirected graph.
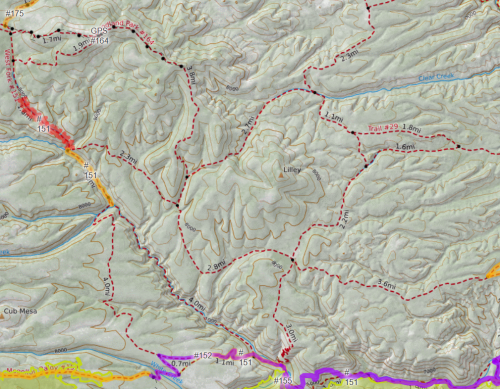
In the next post we will consider how to solve this problem algorithmically, and how the difficulty of computation scales with complexity, and discuss approximations, and discuss how we might write some code to help.