Let us take the tools we developed in the last post and apply to the much larger graph of the Gila National Forest, and see what needs debugging. We follow nearly the same steps as the previous post, so refer to that article for an explanation of why we are taking particular steps in a certain order.
One thing discovered after experimentation is that OSMnx embeds a good deal of geometry information on the attributes of graph edges and graph nodes, so my contract_twos function would need a good deal of modification to correctly join the geometries of two edges to a single edge. Instead, we will use a shortcut. OSMnx has a simplify_graph function, which eliminates all nodes of degree 2, but it can only be used once. (I pray that the maintainers of the OSMnx library might remove that restriction in later releases. ) Before, I used that function just after reading in the OpenStreetMap data, but now we will wait. The trade-off is that we start out with a graph with a huge number of nodes for our initial graphs. Our draw function that can handle OSMnx graphs has an option to show the nodes.
OSMnx version: 1.4.0
NetworkX version: 3.1report(G)
79985 nodes
79983 edges
total length 1546.96 miles
number of zero-degree nodes : 11
number of odd intersections : 900
number of even intersections : 79085
number of 2-way intersections : 79027
number of trailhead/terminus : 489draw(G)
If we turn on display_nodes, we see a jungle of them. The extra nodes slow down calculations, but not too much to bear. (Perhaps I need to display nodes in a higher contrast color than ‘pink’.
We expect some disconnected subgraphs, so choose the largest:
nodes = max(nx.connected_components(H), key=len) J = nx.subgraph(H, nodes).copy() report(J,'in largest subgraph')
30423 nodes in largest subgraph
30493 edges in largest subgraph
total length 631.36 miles in largest subgraph
number of odd intersections in largest subgraph : 262
number of even intersections in largest subgraph : 30161
number of 2-way intersections in largest subgraph : 30155
number of trailhead/terminus in largest subgraph : 67draw(J)
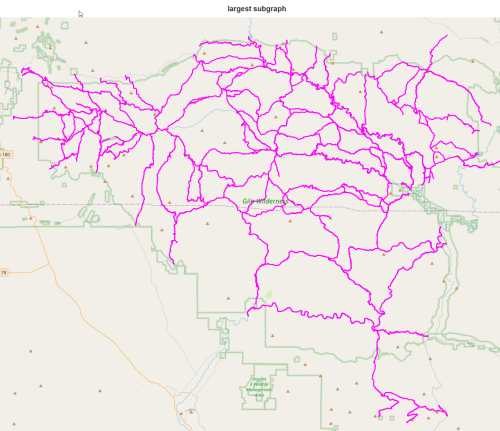
We have lost the entire Aldo Leopold!! Since there is not good connectivity between the Aldo and the rest of the Gila, we will manually add a few roads and cross-country routes in a later post.
delete_ends(J) report(J,'in undirected multigraph with ends removed')
23009 nodes in undirected multigraph with ends removed
23079 edges in undirected multigraph with ends removed
total length 477.01 miles in undirected multigraph with ends removed
number of odd intersections in undirected multigraph with ends removed : 136
number of even intersections in undirected multigraph with ends removed : 22873
number of 2-way intersections in undirected multigraph with ends removed : 22871
number of trailhead/terminus in undirected multigraph with ends removed : 0draw(J)
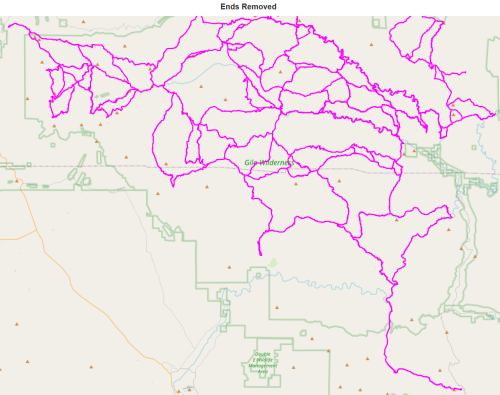
It appears that some ends remain, so let us zoom in and see what is going on.
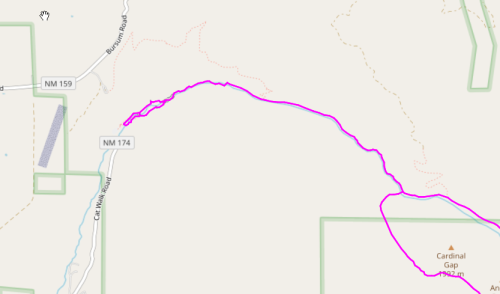
All is revealed. Tiny loops at the trailheads are preventing these dead-ends to be removed, possibly an artifact of GPS tracks. They will not prevent further processing.
Now, instead of using our contract_twos function, we simplify. My code works with multigraphs, but the OSMnx needs a multidigraph, so we convert.
T = J.to_directed() T = ox.simplification.simplify_graph(T, strict=True, remove_rings=True, >>> track_merged=True) J = T.to_undirected() report(J,'with two-nodes merged')
138 nodes with two-nodes merged
211 edges with two-nodes merged
total length 479.91 miles with two-nodes merged
number of odd intersections with two-nodes merged : 136
number of even intersections with two-nodes merged : 2
number of 2-way intersections with two-nodes merged : 0
number of trailhead/terminus with two-nodes merged : 0draw(J, 'Two-nodes merged', show_nodes=True)
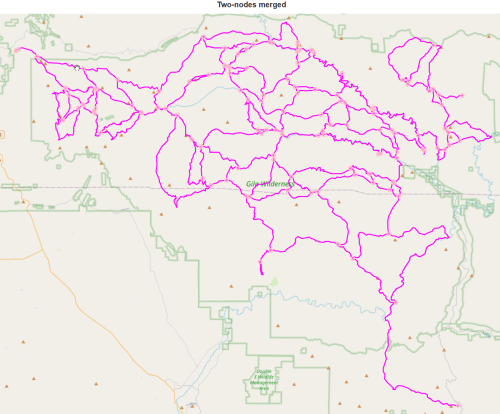
With a much smaller graph, computations should go quicker.
I had to completely re-write the odd_nodes_graph function to preserve node attributes, required for OSMnx plots.
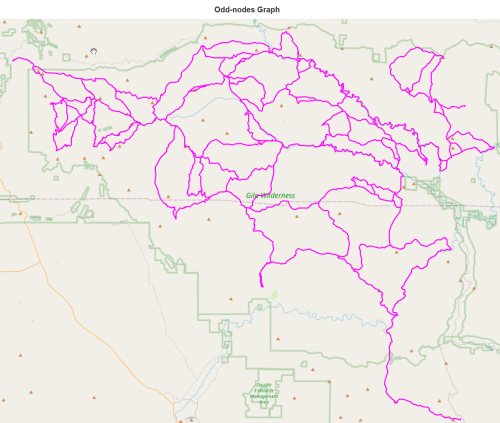
K = odd_nodes_graph(J) report(K,'in odd-nodes graph')
138 nodes in odd-nodes graph
203 edges in odd-nodes graph
total length 455.01 miles in odd-nodes graph
number of zero-degree nodes in odd-nodes graph : 2
number of odd intersections in odd-nodes graph : 128
number of even intersections in odd-nodes graph : 10
number of 2-way intersections in odd-nodes graph : 8
number of trailhead/terminus in odd-nodes graph : 0draw(K,'Odd-nodes Graph')
k_fix_4_list = complete_3node_graph(J,K) report(K,'in odd-nodes 4node bypass')
138 nodes in odd-nodes 4node bypass
215 edges in odd-nodes 4node bypass
total length 529.69 miles in odd-nodes 4node bypass
number of zero-degree nodes in odd-nodes 4node bypass : 2
number of odd intersections in odd-nodes 4node bypass : 136
number of even intersections in odd-nodes 4node bypass : 2
number of 2-way intersections in odd-nodes 4node bypass : 0
number of trailhead/terminus in odd-nodes 4node bypass : 0Finally, find a matching of odd-nodes, to delete edges.
odd_matches_set = nx.algorithms.min_weight_matching(
nx.Graph(K),'length')
print('number of odd matches', len(odd_matches_set))
number of odd matches 68K.remove_edges_from(odd_matches_set) report(K,'with odd-node matches removed')
138 nodes with odd-node matches removed
147 edges with odd-node matches removed
total length 416.63 miles with odd-node matches removed
number of zero-degree nodes with odd-node matches removed : 2
number of odd intersections with odd-node matches removed : 0
number of even intersections with odd-node matches removed : 138
number of 2-way intersections with odd-node matches removed : 125
number of trailhead/terminus with odd-node matches removed : 0draw(K,'Odd-node Matches Removed')
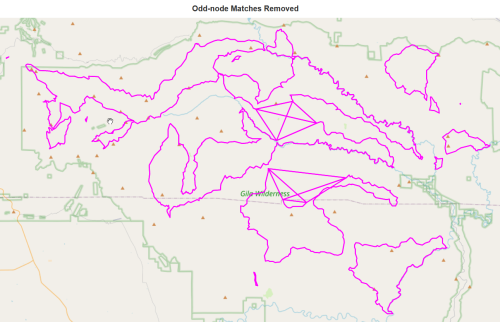
restore_4node_graph(K,k_fix_4_list) report(K,'odd-matches deleted with 4nodes restored')
138 nodes odd-matches deleted with 4nodes restored
143 edges odd-matches deleted with 4nodes restored
total length 366.84 miles odd-matches deleted with 4nodes restored
number of odd intersections odd-matches deleted with 4nodes restored : 0
number of even intersections odd-matches deleted with 4nodes restored : 138
number of 2-way intersections odd-matches deleted with 4nodes restored : 133
number of trailhead/terminus odd-matches deleted with 4nodes restored : 0Finally, we have a graph with no odd nodes. But is it Eulerian? Probably not, because it probably has disconnected subgraphs. Let us find the largest.
nodes = max(nx.connected_components(K), key=len) L = nx.subgraph(K, nodes).copy() report(L,'in largest subgraph with odd-node matches removed')
62 nodes in largest subgraph with odd-node matches removed
63 edges in largest subgraph with odd-node matches removed
total length 154.01 miles in largest subgraph with odd-node matches removed
number of odd intersections in largest subgraph with odd-node matches removed : 0
number of even intersections in largest subgraph with odd-node matches removed : 62
number of 2-way intersections in largest subgraph with odd-node matches removed : 61
number of trailhead/terminus in largest subgraph with odd-node matches removed : 0draw(L,'Largest Subgraph with Odd-Node Matches Removed')
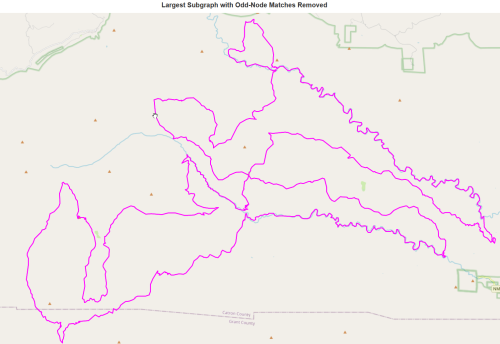
Ouch, about half our network was disconnected. But surely what remains is Eulerian?
if nx.is_eulerian(L):
print('L is eulerian')
print('The node path is: ', [u for u,v in nx.eulerian_circuit(L)])
L is eulerian
The node path is: [2509055489, 2509057123, 2509055502, 9227626167, 2509593307, 2509057094, 2509057647, 2509058481, 2838812812, 2838812805, 2509057291, 2509594712, 2509595144, 2509595627, 2684593045, 2509595676, 9265299803, 2509596122, 2509595984, 2509595742, 3297939898, 9228602425, 9228602417, 2509594941, 2509593423, 2509593401, 9246426895, 2295322477, 2295322644, 4203575729, 4203576270, 2509592348, 2509593141, 2509593702, 2509593769, 2509594051, 2509594354, 2509594518, 2509594155, 2509593307, 2509593113, 2509592624, 2509592557, 2509592346, 4460959741, 2841095147, 9225328740, 2509591310, 2509592149, 2509592316, 9227298570, 2509006103, 2509005336, 2509004799, 2509003844, 2509003421, 2509006359, 2509005827, 2509003928, 2838812547, 2509005592, 2509006101, 2509006233]
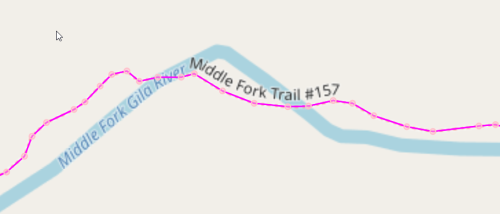
Yay! We have a continuous hiking loop in the Gila that does not repeat any segments. But is it the largest? Probably not. We matched odd nodes with the built-in NetworkX algorithm min_weight_matching, but it is possible another matching gives a longer graph, since we are fighting the problem of disconnected subgraphs. In the next post we show how to iterate through all possible odd-matchings.
But the situation looks hopeful! We found a loop of around 154 miles. And it seems to include some of the best stuff, like the Middle Fork. Perhaps if we add connections to the Aldo, we could push that length closer to 300 miles. And if we add routes into towns and back for resupply, could we possibly get to 400 miles? With a few additional routes (I really liked liking on Bursum Road on the Grand Enchantment Trail) could we push it to 500 miles?
Stay tuned. I am going on my annual long hike, so further coding might have to wait. Source code is here for the brave-of-heart.