My first choice for a programming language for solving our graph problem is Python, with its “batteries included” philosophy, and diversity of native data structures. Data structures such as lists, dequeues, and dictionaries seem more of an afterthought for C++ and Java. My past experience with Python is extremely limited, but I am not on deadline, and can use the brain exercise.

A quick search of graph theory libraries for Python or R turns up NetworkX. The library has built-in solvers for shortest paths, but not necessarily for the longest path we are looking for. But at least I could use their built-in data structures to create my own solver, if necessary.
(In a previous career as a chip designer decades ago, I used awk to solve graph theory problems on huge CMOS netlists because of its built-in associative memory, but let’s stick with a language known to be much more modern and readable, Python.)
An insight about bridges might make our problem easier to solve.
Seven Bridges of Königsberg
Consider these 7 bridges in the ancient city of Königsberg in Prussia. Find a walk through the city that crosses each bridge once and only once.
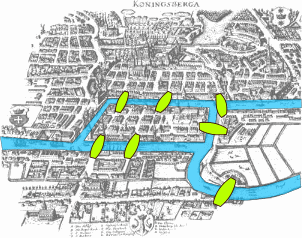
We transform this problem into a graph, where each of 4 land masses is a node, and each bridge is an edge.
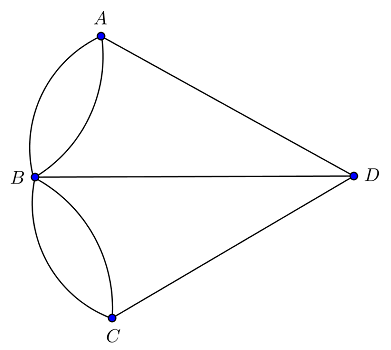
Euler explained that, except for the beginning and end of the walk, whenever you enter a node you must leave the node. So except for the beginning and end, all nodes must have an even number of edges. In this problem, all nodes have an odd number of edges, so a solution is impossible.
An Euler Path is a trail that passes along every edge of graph G exactly once. If the beginning and end nodes are not the same, only two nodes, the beginning and end, have an odd number of edges. All the other nodes must have an even number of edges.
An Euler Circuit is an Euler Path where the beginning and end are the same node, and in this case every node must have an even number of edges.
Euler suggested, but did not prove, that every graph with nodes of an even number of edges has an Euler Circuit. Hierholzer proved this is a sufficient condition in 1873. Hierholzer described an efficient algorithm for finding an Euler Circuit with O(N) complexity, where N is the number of edges.
So perhaps this is good news for our Gila maximum-distance problem. All we need to do is intelligently discard one leg of any three-way intersections, and keep all 4-way intersections, and we know we have a Gila Circuit, that should cover a good percentage of our mapped trails.
The sticking point might be “intelligently discard”.
Referring back to our NetworkX library, and armed with jargon about Euler graphs, we see some useful functions:
eulerian_circuit(G[, source, keys]) Returns an iterator over the edges of an Eulerian circuit in G.
eulerize(G) Transforms a graph into an Eulerian graph.
eulerian_path(G[, source, keys]) Return an iterator over the edges of an Eulerian path in G.
For the Chinese Postman Problem, one tries to convert a graph into a Eulerian graph by reusing (doubling) edges, but trying to add as few edges, or total edge length, as possible. For our original trail problem, this would mean hiking on the same section of trail more than once, which we are trying to avoid.
For the next post, let us try out a bit of computer code on a small fictional trail network, and see what problems we encounter.