Month: June 2023

Let us create a small imaginary trail graph in Python with NetworkX, and play around with plotting and paths. Suppose we have a graph with nodes from 0 to 15:

import networkx as nx
import matplotlib.pyplot as plt

G=nx.Graph()

edges=[(0,1,1),(1,2,1),(2,3,1),(3,4,1),(4,5,1),(5,6,1),(6,7,1),
       (8,3,2),(9,4,1),(9,5,1),(10,7,2),
       (8,9,2),(9,10,2),
       (8,11,2),(12,10,2),
       (11,12,2),(12,13,2),(13,7,2),
       (11,14,2),(14,15,4),(15,13,1)]
G.add_weighted_edges_from(edges)

The tuple (8,11,2) means an edge goes from node 8 to node 11, with weight 2.

Now we specify where the nodes are located.

#pos=nx.spring_layout(G) does not give satisfactory results.
# Draw node positions the hard way.

pos=[(0,4),(1,4),(2,4),(3,4),(4,4),(5,4),(6,4),(7,4),
     (1,3),(3,3),(5,3),
     (3,2),(6,2),(8,2),
     (4,1),(7,1)]

We are almost ready to draw the network. Since we want to draw weights for the edges, we have an extra step.

options = {
    "font_size": 16,
    "node_size": 1000,
    "node_color": "white",
    "edgecolors": "black",
    "linewidths": 5,
    "width": 5,
}
nx.draw_networkx(G, pos,**options)

labels = {e: G.edges[e]['weight'] for e in G.edges}
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels, font_color="red")
plt.show()

And here is our result.

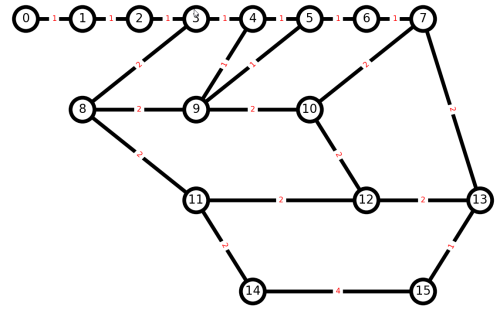
Think how we can convert this into a Euler graph, so all nodes have an even number of edges. We can try a Networkx library function, but should not expect it will do what we want, because it will create a multigraph, with more than one edge between nodes.

Continue reading “Trails and Graph Theory 3: NetworkX”

My first choice for a programming language for solving our graph problem is Python, with its “batteries included” philosophy, and diversity of native data structures. Data structures such as lists, dequeues, and dictionaries seem more of an afterthought for C++ and Java. My past experience with Python is extremely limited, but I am not on deadline, and can use the brain exercise.

A quick search of graph theory libraries for Python or R turns up NetworkX. The library has built-in solvers for shortest paths, but not necessarily for the longest path we are looking for. But at least I could use their built-in data structures to create my own solver, if necessary.

(In a previous career as a chip designer decades ago, I used awk to solve graph theory problems on huge CMOS netlists because of its built-in associative memory, but let’s stick with a language known to be much more modern and readable, Python.)

An insight about bridges might make our problem easier to solve.

Seven Bridges of Königsberg

Consider these 7 bridges in the ancient city of Königsberg in Prussia. Find a walk through the city that crosses each bridge once and only once.

We transform this problem into a graph, where each of 4 land masses is a node, and each bridge is an edge.

Euler explained that, except for the beginning and end of the walk, whenever you enter a node you must leave the node. So except for the beginning and end, all nodes must have an even number of edges. In this problem, all nodes have an odd number of edges, so a solution is impossible.

Continue reading “Trails and Graph Theory 2: Bridges”

It all started with a question:

What is the longest continuous route on existing trails in the Gila National Forest, that does not repeat any segment (but intersections are OK)?

And what is the longest continuous loop?

Can the result be mapped and documented as a Long Trail to share with hikers?

Sagebrush

The Gila has a few trails that dead-end, so those can be eliminated, and several trails are currently in poor condition due to fire or lack of maintenance, and not reasonable to hike. Furthermore, some trails are not where they are shown on published maps. Fortunately, I know an expert on the Gila, an individual with boundless energy who is dedicated to reopening and maintaining routes. And perhaps another published long trail could be used as a motivation to go out and work on particular segments.

Finding a longest route is an optimization problem, so mathematics might be able to help. A famous problem in math is the Traveling Salesman. One version:

A salesman needs to visit all lower-48 state capitals and return to the beginning. What is the route with minimum distance?

An obverse is the Longest Path Problem

What is the longest path in a given network?

Nano Intro to Graph Theory

Continue reading “Trails and Graph Theory: Graphs”